CS스터디

[CS스터디] Balanced Tree(AVL,RBT)

by VICENTE97P4

March 27, 2022, 11:49 a.m.

Balanced Tree

tree가 양쪽으로 균형있게 분포될 수 있게 insert, delete 할 때마다 자동으로 트리의 height를 조정하는 트리입니다.

한마디로 균형을 유지하는 tree를 의미합니다.

tree가 치우치지 않아 조회 시 최악의 시간복잡도를 피할 수 있습니다.

AVL, Red-Black Tree, B트리, B+트리 등이 있습니다.

AVL(Adelson-Velskii and Landis)

기본적으로 BST입니다.

왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 최대 1까지 나는 것을 허용합니다.

조회, 삭제와 삽입은 BST와 똑같이 O(h)입니다. 하지만 BST는 O(h)가 O(n)이 될 수도 있지만 AVL은 O(logn)이 보장되죠.

삽입과 삭제 과정은 일반 BST와 같습니다. 하지만 그 후에 balancing 과정이 추가되었고, 매우 복잡하죠.

Balancing은 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 2 이상일 때 발생합니다.

balancing이 발생하는 경우는 크게 4가지입니다. 복잡하지만 하나씩 봅시다.

1. LL, RR -> Single Rotation

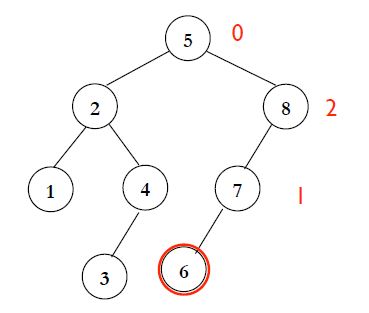
LL은 왼쪽 자식의 왼쪽 서브트리의 높이가 더 높은 경우입니다.

위 그림에서는 6이 새로 삽입되었을 때 노드 8의 입장에서는 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 2가 됩니다.

그럼 8 입장에서 6의 위치는 왼쪽 자식인 7의 왼쪽 서브트리에 삽입된걸로 보입니다.

네, 그러니까 삽입된 위치의 부모의 부모(grand parent) 관점에서 LL, LR, RL, RR을 구분합니다.

이는 당연합니다. 왜냐하면 높이 차이가 2 이상이 될 때 balancing이 발생하는데,

삽입된 노드의 바로 위 부모에서는 높이 차이가 많이 나야 1이 납니다.

그러니 부모의 부모의 입장에서 분류하는게 당연하죠.

아무튼 LL, RR같이 일직선으로 노드가 위치해있다면 차라리 편합니다.

한 번의 회전(single rotation)으로도 balance를 맞춰줄 수 있기 때문이죠.

위 그림에서 6-7-8을 오른쪽으로 회전시켜서 8 자리에 7을, 원래 있던 8은 7의 right child로 두면 됩니다.

즉, LL의 경우에는 오른쪽, RR의 경우에는 왼쪽으로 회전시키면 됩니다. 그럼 새로 붙은 방향의 자식이 새로운 부모가 되죠.

높이차이가 2 이상 나는 노드에서 LL인 경우는 왼쪽 자식이, RR인 경우에는 오른쪽 자식이 새로운 부모가 됩니다.

당연하죠.. 차이가 나니까 그 쪽 높이가 짧아져야 하니까요..

이렇게요.

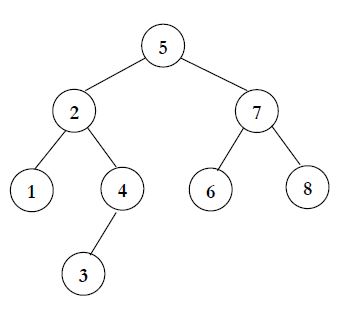
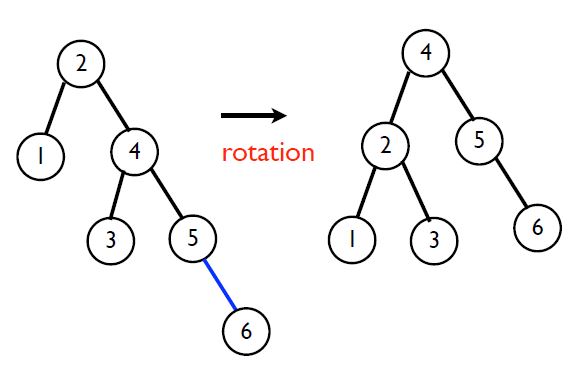
그런데 만일 새로운 부모가 될 노드가 child가 2개 모두 있는 경우는 어떡하냐?

예를 들면 다음과 같은 경우죠.

위 경우에는 2의 입장에서 보면 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 2가 나게 됩니다.

그러면 2의 입장에서 6의 위치는 4의 오른쪽, 그러니 RR이니까 왼쪽으로 rotation 시켜줘야 합니다.

그런데 어랍쇼? 4가 left child가 있어서 회전하면 뭔가 이상해지는데요?

이럴 경우는 left child를 부모노드인 2의 오른쪽에 붙여주고 회전시키면 됩니다.

그럼 위 그림처럼 회전이 완성되죠.

즉, 새로운 부모가 될 노드에, 회전하려는 방향에 child가 있다면 그 child를 회전 전 부모에 달아주면 됩니다.

RR이라 왼쪽으로 회전할 때는, left child를 부모 노드의 right child로,

LL이라 오른쪽으로 회전할 때는, right child를 부모 노드의 left child로,

이러면 BST의 특징을 깨지 않고 balance를 유지할 수 있습니다.

2. LR, RL(Double rotation)

이 경우는 조금 더 복잡합니다. 회전을 2번 해야 합니다.

높이차이가 2 이상 나는데, 내 왼쪽 자식의 오른쪽 서브트리, 또는 오른쪽 자식의 왼쪽 서브트리가 높이가 큰 경우입니다.

그럴 경우는 한 번 회전시켜줘서 LL, RR로 만들어주고, 위에서 본 LL, RR 회전을 이용하는 겁니다.

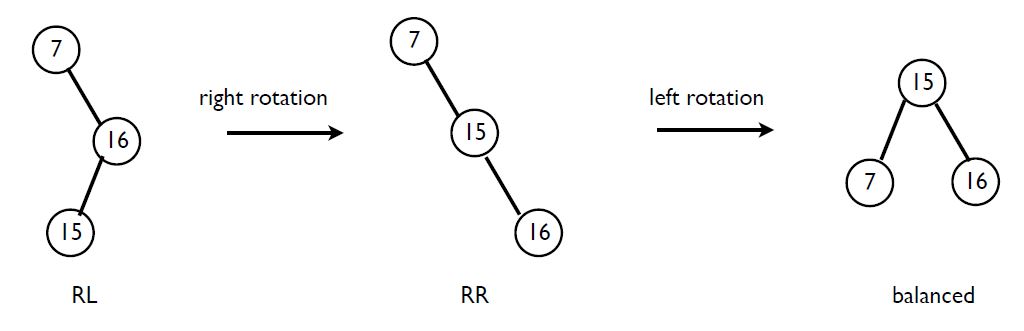
7 입장에서 15는 오른쪽 자식(16)의 왼쪽 서브트리에 있으니 RL입니다.

그럼 한 번 오른쪽으로 회전시켜서 RR을 만들어주고, RR 회전을 하면 됩니다.

LR인 경우에는 왼쪽으로 회저시켜서 LL을 만들어주고, LL회전을 하면 됩니다.

회전하는데 자식이 걸릴 경우도 보겠습니다. LL, RR 때와 방식은 같습니다.

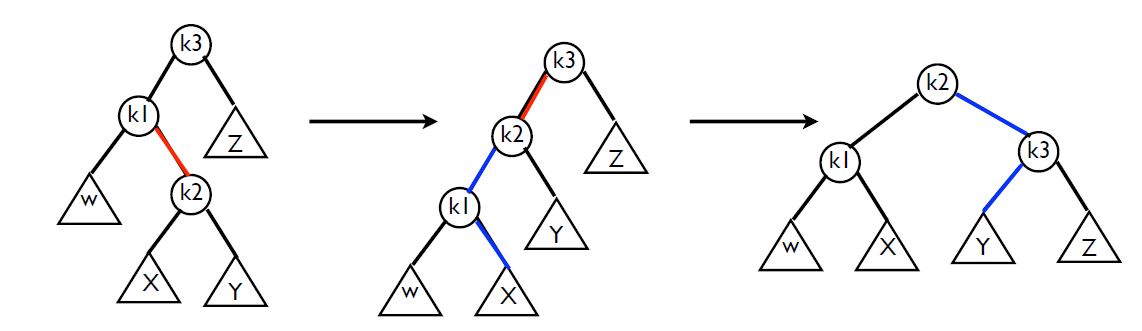
k3 입장에서 왼쪽 서브트리의 높이가 2 큽니다. 그리고 k2가 LR에 위치해있기 때문에 왼쪽으로 한 번 회전해서 LL을 만들어줍시다.

이때, k2가 회전하는 왼쪽 방향인 왼쪽 child가 있습니다. 그냥 k2를 부모노드로 올려주고 왼쪽 서브트리인 X를 k1의 오른쪽에 달아주면 됩니다.

그리고 k2의 왼쪽은 비게 되고, 그 빈 자리에 k1을 달아주면 됩니다.

그리고 이제 오른쪽으로 한 번 회전해야 하는데, 역시 부모가 될 k2 노드에 오른쪽 서브트리(Y)가 있습니다.

그럼 그냥 오른쪽 서브트리 Y를 k3의 왼쪽에 달아주고 k2가 오른쪽에 k3를 달아주면 됩니다.

이런 방식이면 BST를 유지할 수 있습니다.

LR, RL의 경우는 처음 회전 때는 높이 차이가 2 이상 나는 노드(k3)는 회전에 포함되지 않습니다.

두 번째 회전 때 포함되고 부모노드가 바뀌게 됩니다.(k3 -> k2)

Red-Black Tree

얘 역시 BST의 일종입니다.

그런데 모든 노드가 검정색 또는 빨간색으로 색칠되어있죠.

red-black tree에서는 말단에 null 대신 external node라는게 있다고 가정합니다.

그리고 이 external node는 검정색입니다.

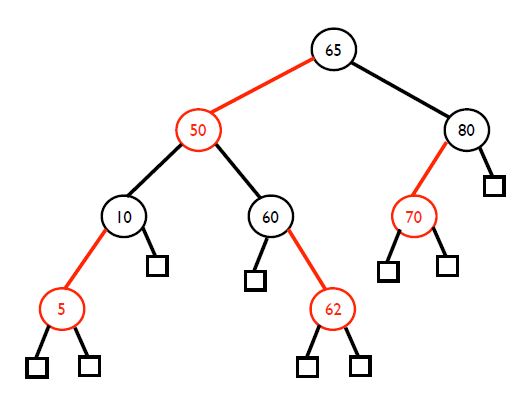
위 그림에서 검은 네모가 external node입니다.

이 red-black tree에는 몇가지 조건이 있습니다.

1. root와 external nodes는 검은색이다.
2. red node는 연속적으로 이어질 수 없다.
3. 모든 internal-node에서 external node까지의 경로에서 검은 노드의 개수가 같아야 한다.

1, 2번은 그냥 그러려니 하겠는데 3번이 좀 어지럽습니다.

그냥 루트에서 모든 leaf node까지 갈 때 각 경로마다 거쳐가는 검은 노드의 개수가 같아야 한다고 이해하면 됩니다.

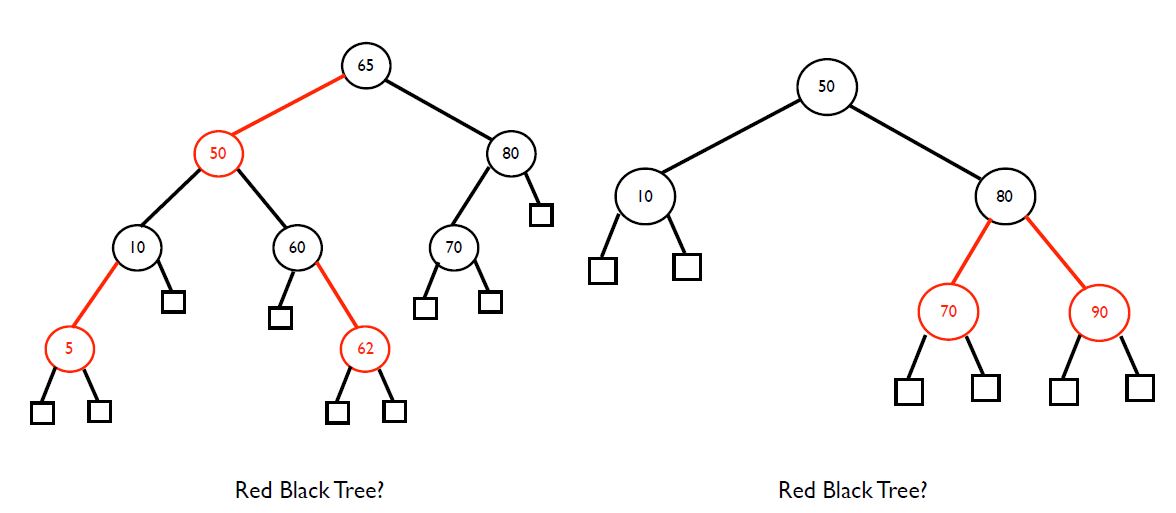
왼쪽은 red black tree가 아닙니다.

왜냐하면 루트인 65 에서 왼쪽 서브트리의 leaf node까지 갈 때 검은 노드를 총 2번 거칩니다.(external node까지 합치면 3번인데 어차피 external node는 공통되니 편의상 제외시켜줍시다.)

그런데 오른쪽 서브트리의 leaf node까지 갈 때는 70까지 가는 경우 검은 노드를 총 3번 거칩니다. 그래서 red black tree가 아닙니다.

반면, 오른쪽은 red black tree입니다. leaf node까지 거쳐가는 black node의 개수가 2개로 동일하고, 연속되는 red node도 없습니다. 루트 또한 black이구요.

rank는 black height라고도 합니다.

어떤 노드에서 external node까지 경로에 있는 black pointer의 개수입니다.

external node는 black pointer가 없으니 rank가 0입니다.

그럼 어느 두 서브트리의 높이는 최대 몇 배까지 차이날 수 있을까요?

정답은 2배입니다.

루트에서 왼쪽 서브트리의 높이를 P, 오른쪽 서브트리의 높이를 Q라고 하면

length P <= 2 * length Q

위 식이 성립할 수 있습니다.

이유는 간단합니다. Q가 black node로만 이루어져있고, P가 black과 red가 번갈아가면서 나온다면 최대 2배까지 차이날 수 있습니다.

어느 루트노드의 rank를 r, internal node의 개수를 n, 높이를 h라고 해봅시다.

- h <= 2*r 입니다.

위에서 이야기 한 것과 같은 원리입니다. rank는 black node의 개수인데, 높이는 red node까지 세어주기 때문에 높이는 rank의 최대 2배까지 가능합니다.

- n >= 2^r - 1

internal node의 개수는 적어도 2의 rank 승 - 1 만큼은 있다는 의미입니다.

rank는 leaf node까지 갈 때 거치는 black node의 개수입니다.

아래로 내려갈수록 branch 개수가 2배씩 커질 수 있는데 rank가 1 커지면 반드시 internal node는 2배씩 많아집니다.

1 + 2 + 2^2 + ... + 2^(r-1) = 2^r - 1 이죠.

그렇지 않은 경우, root node에서 leaf node까지 갈 때 거쳐가는 black node의 개수가 달라지기 때문입니다.

그리고 n에는 black internal node 뿐만 아니라 red internal node 또한 있으니 위 식은 성립합니다.

- h <= 2log(n+1)

위 식은 당연하니 따로 설명하지 않겠습니다.

여하튼 RBT의 조회, 삽입, 삭제의 시간복잡도는 O(logn)입니다.

Insert

insert 과정을 살펴보겠습니다.

1. 일단 그냥 BST처럼 삽입합니다.
2. 그 다음 빨강으로 칠합니다.
3. 마지막으로 red-black tree의 특성을 만족하도록 트리를 수정합니다.

1, 2번은 뭐.. 그냥 하면 되는데 3번이 골때립니다.

일단 새로 칠하는 노드는 무조건 빨간색입니다. 그래서..

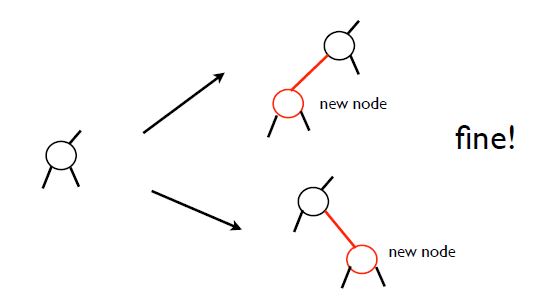
1. 부모노드가 검은색인 경우는 그냥 삽입한 노드를 색칠만 빨강으로 해주면 끝입니다.

이 경우는 간단한데.. 문제는 삽입한 노드의 부모 노드가 빨간색일 경우입니다.

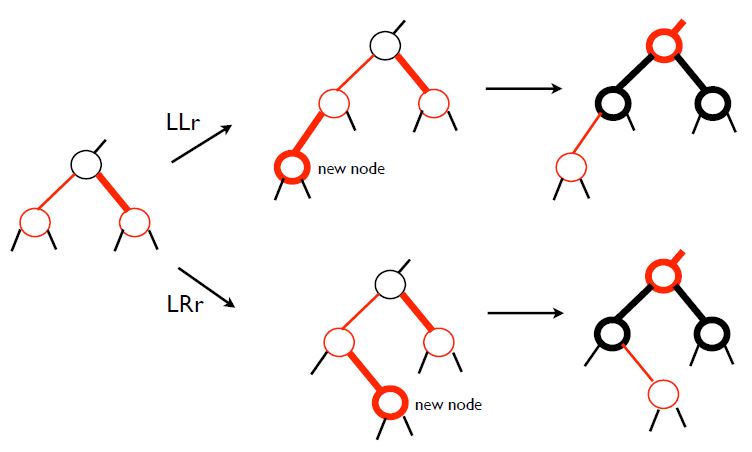
2. LLr, LRr, RLr, RRr

AVL 때와 마찬가지로 부모의 부모 관점에서 봤을 때 left와 right를 결정합니다.

r은 삽입한 부모 노드의 sibling의 색깔을 의미합니다. sibling도 빨강일 경우입니다.

그런데 이 경우는 간단한 것이, 그냥 자식과 새로 삽입한 노드가 모두 빨간색이기 때문에

AVL처럼 회전 방향이 바뀌고 그런게 없습니다. 그냥 삽입한 노드의 부모 노드와 sibling node의 색깔만 검정색으로 바꿔주면 됩니다.(recoloring)

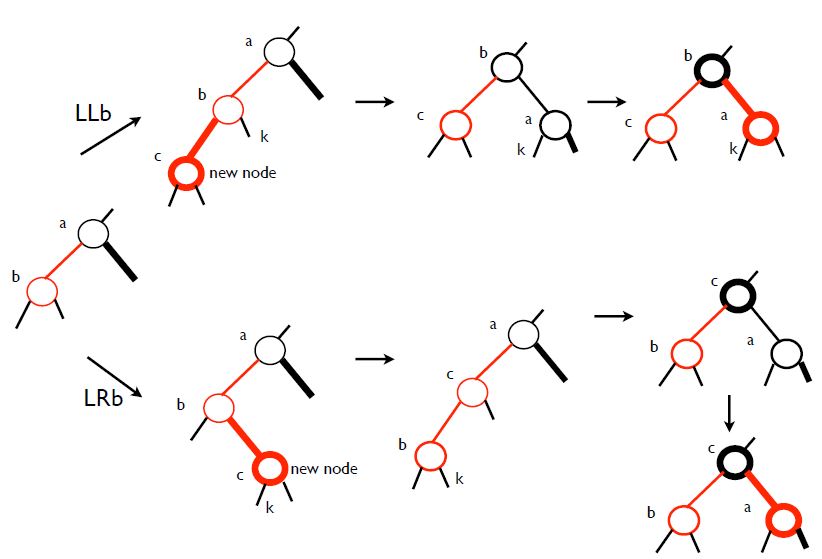
3. LLb, LRb, RLb, RRb

이 경우가 골때립니다.

삽입한 노드의 부모는 빨간색인데, 부모의 sibling은 검은색인 경우입니다.

이 경우에는 결국 rotation이 일어납니다.

그런데 AVL에서 본 바와 같이 LR, RL인 경우에는 일단 첫 번째 회전을 통해 LL과 RR로 만들어주고 회전을 한 번 더 해서 총 2번 해줍니다.

LL과 RR인 경우는 한 번만 회전해주면 되죠.

그리고 나서, 새롭게 올라온 부모는 검정색, 두 자식의 색깔은 모두 빨간색으로 칠해줍니다.

AVL을 충분히 이해하셨다면 이 과정도 그렇게 어렵지는 않을 것이라 생각합니다.

recoloring이 헷갈리실 수 있는데 삽입 때는, sibling이 빨간색이면 rebalance 후 부모가 빨간색, 검은 색이면 부모도 검은색이라 생각하시면 편합니다.

Deletion

BST와 지우는 과정은 같습니다.

역시 지우고 나서 red black tree의 조건을 맞추는 것이 까다롭습니다.

빨간 노드를 지운 경우

이 경우에는 rebalancing이 필요없습니다. rank가 바뀌지 않았기 때문이죠.

검은 노드를 지운 경우(이게 진짜 골때립니다.)

경우를 나눠서 차분히 보겠습니다.

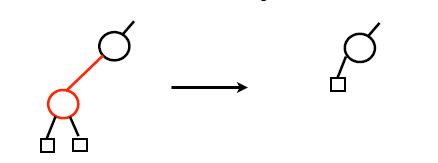
1. 만일 single-child parent를 지운다면, 그 노드는 무조건 검은색이다.

child는 어차피 빨강이니까 그냥 이식해주고 빨강을 검은색으로 바꿔주면 된다.
2. 자식이 2개인 경우에는..
- BST때와 같이 왼쪽 서브트리의 가장 오른쪽 노드, 또는 오른쪽 서브트리의 가장 왼쪽 노드를 지워준다.
-- 그 지울 노드가 빨간색이면 그냥 지운다.
-- 만약 부모가 하나밖에 없으면 1번 규칙을 적용한다.
- 근데 지울 노드가 black leaf라면.. 경우가 복잡해진다..

1번부터 봅시다.

사실 차분히 생각하면 충분히 알 수 있습니다.

single-child parent라면 빨간색일 수 없습니다.

왜냐하면 그럴 경우 child는 반드시 black node가 되며, root에서 모든 leaf node까지 갈 때 거치는 black node 수가 single-child parent의 child를 방문할 때 반드시 1개 이상 커지기 때문입니다.

이제 지울 노드가 black node일 경우를 봅시다..

참고로 여기서는 노드 1개가 아닌 서브트리로 봐야 합니다.

v는 단순한 노드 1개가 아닌 삭제가 일어나서 rank가 1 모자란 서브트리입니다.

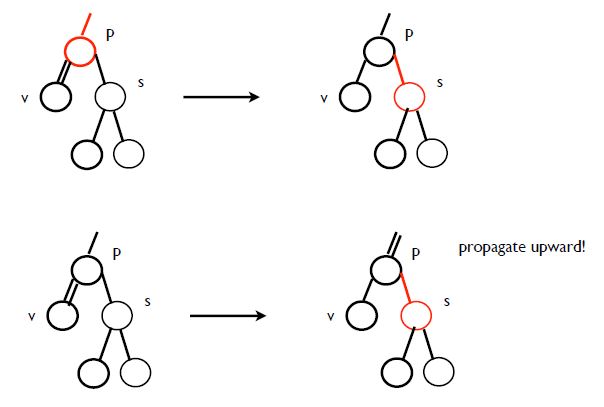
1. 지운 노드의 sibling이 black, black child만 가지는 경우

지운 노드의 sibling이 black이고 black child를 가진 경우입니다.

일단 v는 지금 sibling인 s에 비해 rank가 1 부족합니다. 그래서 s의 rank를 낮춰주거나 v의 rank를 올려줘야 합니다.

여기서는 s의 rank를 낮추는 것이 가능하고, 또 간단합니다.

이 경우에는 부모노드를 black으로 바꿔주고 sibling을 red node로 바꿔주면 됩니다.

두 줄 표시는 rebalancing을 해야 한다는 표시입니다. 이 과정을 거치면서 두 줄을 위로(부모쪽으로) 전파해나갑니다.

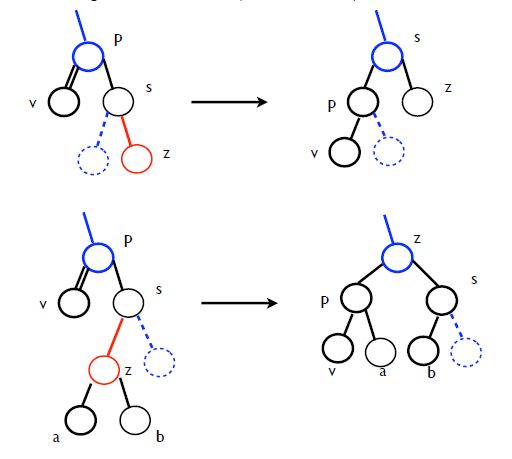
2. 지운 노드의 sibling이 black, red child가 있는 경우

v의 rank가 1 부족한데 s의 child에 red가 있어서 v의 rank를 1 늘려주는 것이 해결책입니다.

이 경우에는 LL, RR, LR, RL rotation이 발생합니다.

이때 파란색은 빨강, 검정 모두 될 수 있다는 의미이며, 점선은 노드가 있을 수도, 없을 수도 있다는 의미입니다.

아니, 첫번째 그림은 v가 rank 1만큼 더 많은데요? 이럴 수 있는데 v는 지금 서브트리에서 1개를 지워서 rank가 1 모자란 상태입니다.

그래서 p를 부모로 두어 rank를 1 늘려줘야 z와 rank가 같습니다.

두 번째 그림에서는 아니 왜 점선이죠? 무조건 있어야 s의 rank가 말이 되는데요? 이러실 수 있습니다.

그런데 여기서는 rebalance 전에는 이미 balanced된 부분이기 때문에 그렇게 표시한 것입니다.

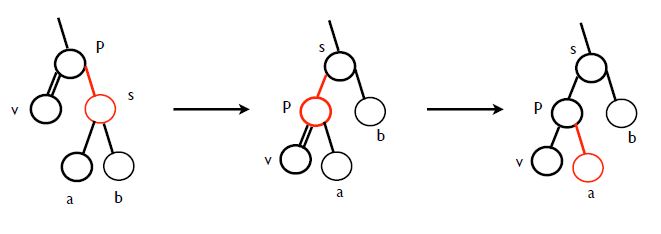
3. 지운 노드의 sibling이 red인 경우

v는 지금 rank가 1개 모자란 상태이므로 하나를 땡겨와야 합니다.

그래서 v쪽으로 회전시켜준 뒤, v의 sibling에 red를 칠해줍니다.

그러면 생각했을때, v는 1개 모자라니까 그렇다 치고, 아니 그럼 p의 right child rank가 안맞는데? 이러실 수 있습니다.

그런데 a는 원래 rank가 v보다 하나 많은 서브트리였습니다. 그런데 p를 하나 부모로 뒀기 때문에 rank가 하나 늘어났습니다.

그래서 a를 red로 칠해주어 v와 rank를 맞춰주는 것입니다.

RBT는 parent, sibling, sibling의 자식의 색깔까지 고려해서 경우를 나눠서 매우 복잡했습니다.

sibling까지 고려하는 이유는 rank를 맞춰주기 위함이었죠.

AVL, RBT는 in-memory 종류의 hash에서 쓰입니다.

AVL, RBT은 balancing factor가 |1|이기 때문에 삽입 삭제가 빈번한 경우보다는 조회가 자주 일어나는 경우에 쓰이면 좋습니다.

삽입 삭제가 많이 일어나면 balancing이 자주 일어날 확률이 높기 때문이죠.

그렇기에 DB 보다는 in-memory에 주로 쓰입니다.

DB 작업은 cost가 큰 편인데, DB에서 balancing 작업이 빈번히 일어나면 DB에서의 작업이 길어지기 때문입니다.

Java에서 Hash를 구현할 때 collision이 발생하면 separate chaining 방식을 사용합니다.

이때 chain에 8개 이상의 원소가 걸리면 RBT를 사용하여 조회 시간을 log로 줄인다고 합니다.

AVL이 RBT보다 엄격하게 높이 차이를 관리합니다. 그래서 balancing이 더 자주 일어나게 됩니다.

그래서 AVL은 삽입 삭제보다는 조회가 많이 일어나는 경우에 효율적이고, RBT는 그보다는 유연하다고 볼 수 있죠.

하지만 이 또한 AVL에 비하자면 그렇다는 것이지 RBT 또한 삽입 삭제가 빈번히 일어나는 경우보단 조회가 많을 때 더욱 효과적입니다.

collision 해결법

open addressing, linked list 중 data가 적다면(collision이 적다면) separate chaining보다 open addressing이 더 효율이 좋다.(spatial locality)

JAVA에서는 8개부터 linked list를 RBT로 변경하고, 6개가 되면 다시 linked list로 바꾼다.

차이값이 8 -> 7이 아닌 8 -> 6인 이유는 잦은 linked list와 RBT로의 변환을 통한 성능저하를 막기 때문이다.

hash join

방법, 키는 어떤 걸로? 어떤 테이블로 해시 만들어야 하는지? 이때는 open addressing이 좋을지 chaining이 좋을지?

PK일 경우에는 collision이 상대적으로 적으므로 open addressing,

그 외에는 collision 되는 경우가 많으므로 chaining

Heap

배열로 구현시 장점

링크드 리스트로 만들었을 때 Heapify 가능 여부, 되어있을 때 heap sort 성능

면접 질문 정리: https://velog.io/@minsgy/%EB%B0%B1%EC%97%94%EB%93%9C-%EA%B0%9C%EB%B0%9C%EC%9E%90-%EB%A9%B4%EC%A0%91%ED%95%99%EC%8A%B5%EB%82%B4%EC%9A%A9#%EB%94%94%EC%9E%90%EC%9D%B8-%ED%8C%A8%ED%84%B4

62 view 803

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

SkumUJSQ

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1 OR 2+145-145-1=0+0+0+1

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1 OR 3+145-145-1=0+0+0+1

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

*if(now()=sysdate(),sleep(15),0)

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

0'XOR(
*if(now()=sysdate(),sleep(15),0))XOR'Z

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

0"XOR(
*if(now()=sysdate(),sleep(15),0))XOR"Z

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1); waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1 waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

M2hEwfWV'; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1 OR 449=(SELECT 449 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1) OR 207=(SELECT 207 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

-1)) OR 762=(SELECT 762 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

UdOEVtzo' OR 245=(SELECT 245 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

AsXDSAd9') OR 769=(SELECT 769 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

RSRgEZJX')) OR 711=(SELECT 711 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

*DBMS_PIPE.RECEIVE_MESSAGE(CHR(99)||CHR(99)||CHR(99),15)

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||'

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

��%2527%2522\'\"

Updated: Feb. 22, 2025, 5:28 p.m.

fnfOzvSR Feb. 22, 2025, 5:28 p.m.

@@WWuYF

Updated: Feb. 22, 2025, 5:28 p.m.