Algorithm

백준 18251번: 내 생각에 A번인 단순 dfs 문제

by VICENTE97P4

May 12, 2022, 2:32 p.m.

문제 링크: https://www.acmicpc.net/problem/18251

정말 오랜만에 알고리즘 문제풀이로 돌아왔습니다.

졸업 프로젝트 하느라, 학교 공부 하느라, 또 CS 스터디 하느라 삶이 너무 피폐했었네요..

해도 해도 부족한 부분이 많아서.. 끝이 없는 것 같습니다.

이 문제는 그냥 제목이 재밌어서 풀어보게 되었습니다.(python)

문제 이름이 길어서 제목에는 짤려서 나오는데, 부제에는 풀네임으로 나옵니다.

이 문제 하나만 몇 시간씩 뚫어져라 쳐다보면서 '어쩌라는 거지..' 하면서 고민했던 기억이 있습니다.

풀고 나서 머리가 저렸지만 그래도 출근해서 열심히 문제 풀고 퇴근했던 그때가 가장 행복했던 시절이 아니었나 싶네요.

근데 아무리 봐도 A번이 되기에는 시간복잡도도 괴랄하고 어렵지 않나.. 하는 생각이 듭니다.

이번 문제는 어렵습니다.

일단 머리 아픈 트리가 나오는데, 트리의 연결이 주어지지 않고, 좌표도 주어지지 않습니다.

게다가 연속합을 트리에다가 적용해야 하는데, 트리는 1차원 배열과 달리 2차원이기 때문에

'사각형을 어떻게 쳐야하지?' 하는 생각이 듭니다.

일일히 사각형을 다 쳐버리면 분명히 시간초과가 날껍니다. 애초에 N^2 접근 자체가 안됩니다.

입력값이 262,143 이기 때문입니다. 통상 입력값이 10000이 넘으면 N^2 으로는 풀리지 않습니다.

(프로그래머스는 간혹 10000이 N^2으로 풀리기도 합니다.)

그렇다고 사각형의 범위를 정하지 않으면 답을 구할 별다른 수도 없긴 합니다.

사각형의 높이에 따라 포함이 될 수 있는 y값과 그렇지 않은 y값 혹은 너비에 따른 x값이 정해져있기 때문입니다.

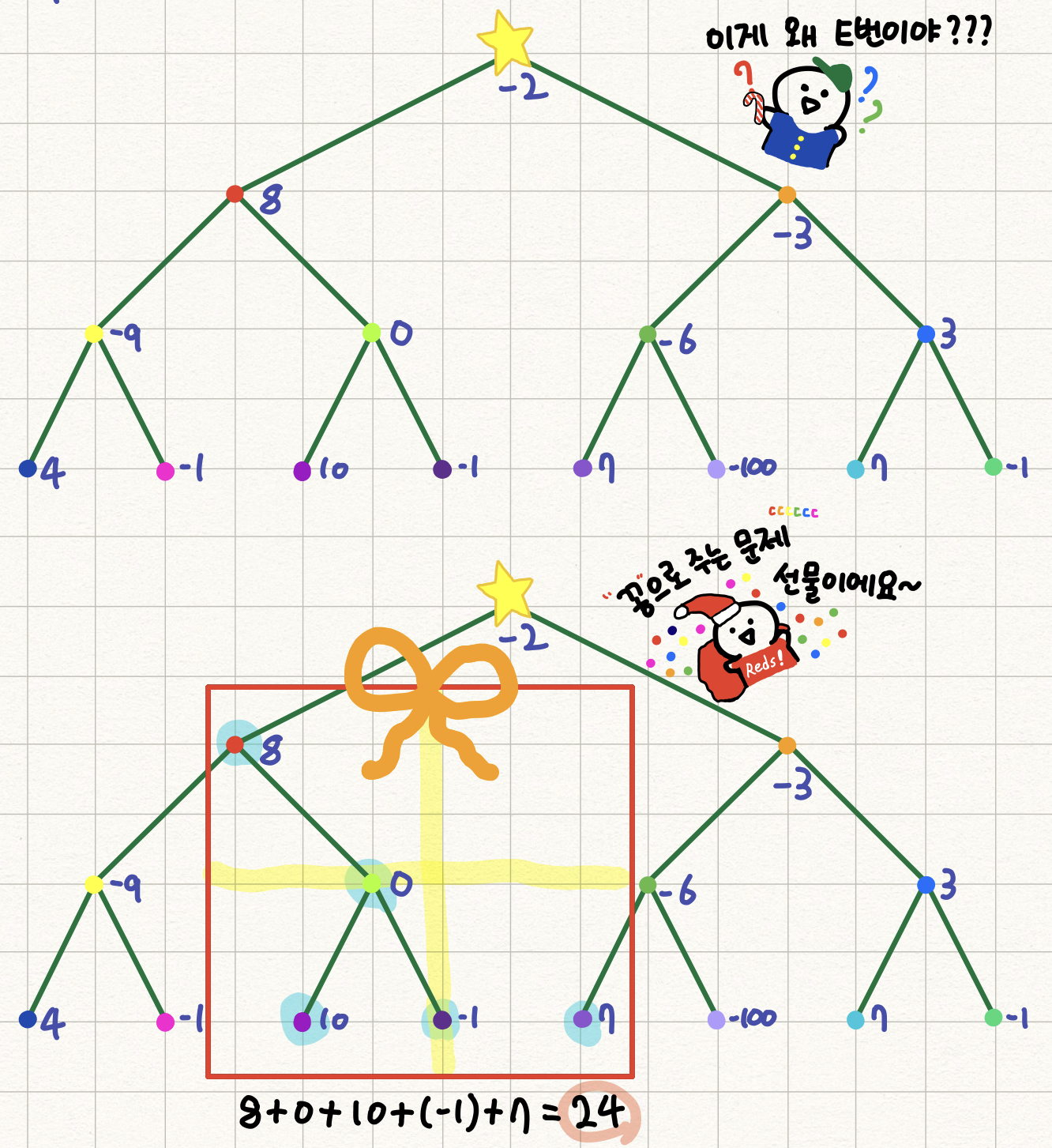
(귀여운 요정이 기만 가득한 말들을 하니까 킹받네요 ^^ 이게 어떻게 꽁입니까..)

위에서 주저리 주저리 설명했지만 이 문제가 어려운 이유는 일반적인 1차원 연속합 문제와 달리

2차원이기 때문입니다. 즉, x, y 2개가 있기 때문입니다.

그럼 x와 y 중 1개를 고정시키면 우리가 아는 1차원 연속합 문제로 바뀝니다.

그리고 그 고정하는 범위를 변화시켜서 모든 경우를 계산해주면 정답을 구할 수 있습니다.

그런데 그러면, x와 y 중 어떤 값을 고정시키고 변화시킬까요?

당연히 y값을 고정시켜야 합니다. 왜냐하면 트리이기 때문에 높이가 log scale이 되어서 짧기 때문이죠.

무슨 말인지는 예를 보면서 알아봅시다.

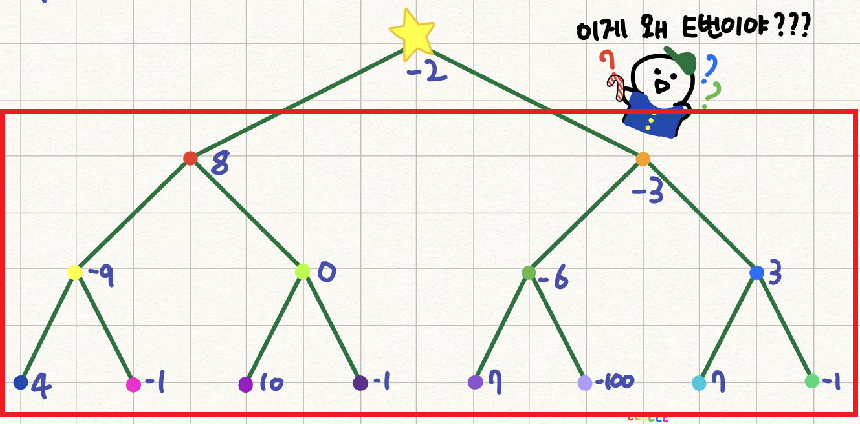
y값의 범위를 이렇게 포함하도록 고정시켰다고 합시다.

그럼 제일 왼쪽에 있는 노드부터 연속합을 적용해가면 됩니다.

합이 음수가 되면 0부터 다시 시작하고, 양수면 계속 들고가면서 최댓값 비교를 합니다.

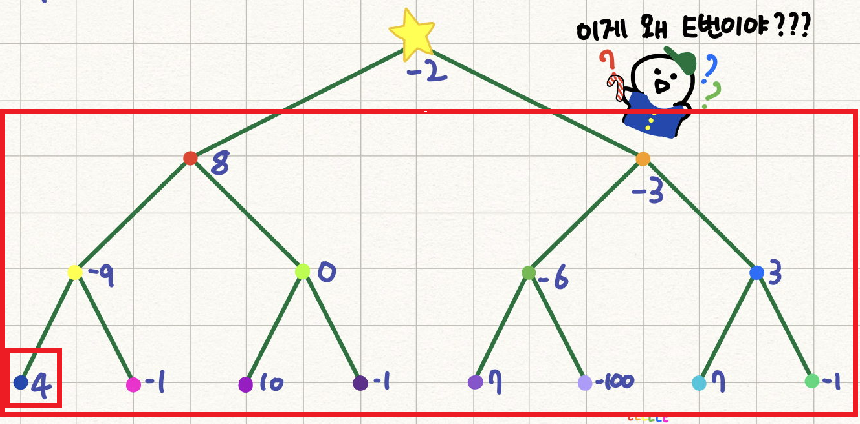
4를 일단 포함시켜봅시다. 현재 최댓값은 4입니다.

현재까지의 합을 s라고 하면 s는 4입니다.

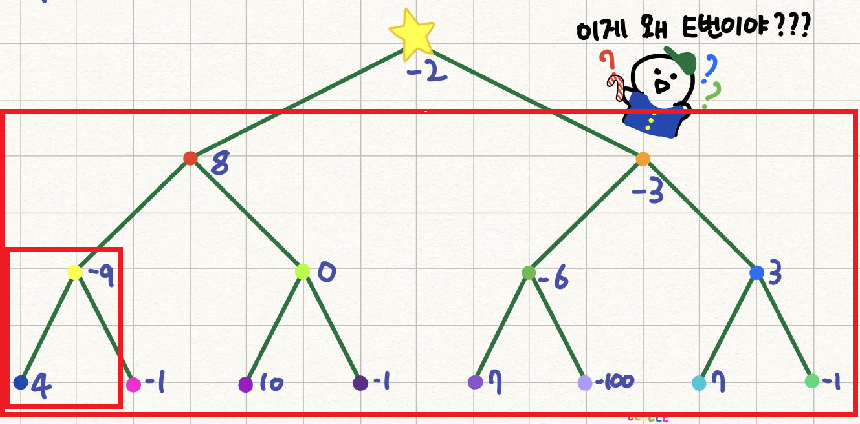
-9까지 더해봅시다. 4 - 9 = -5입니다.

음수이니까 다시 현재까지의 합 s를 0부터 다시 시작하고,

최댓값 4보다 작으니 최댓값 갱신은 이루어지지 않습니다.

8을 만났으니 현재까지의 합 s는 8입니다.

양수이니 계속 s를 유지하고, 최댓값 4보다 크니 최댓값을 8로 갱신시켜줍니다.

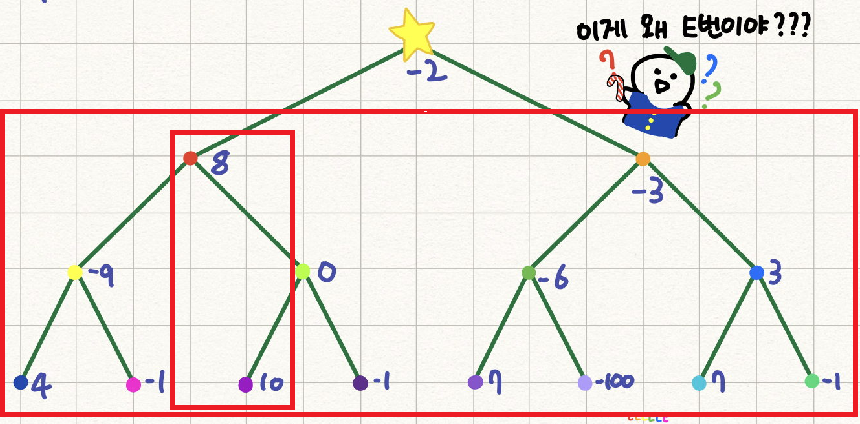
10을 만나서 s는 18이 되고 최댓값 역시 18이 됩니다.

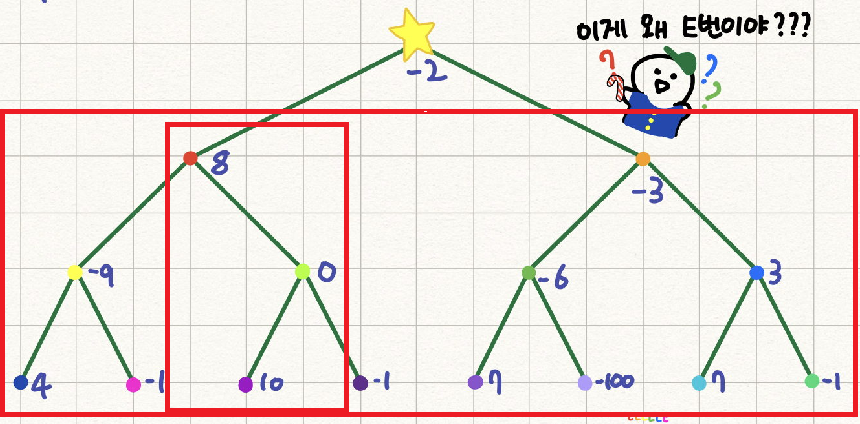
0을 만났으니 s는 18, 최댓값도 18입니다.

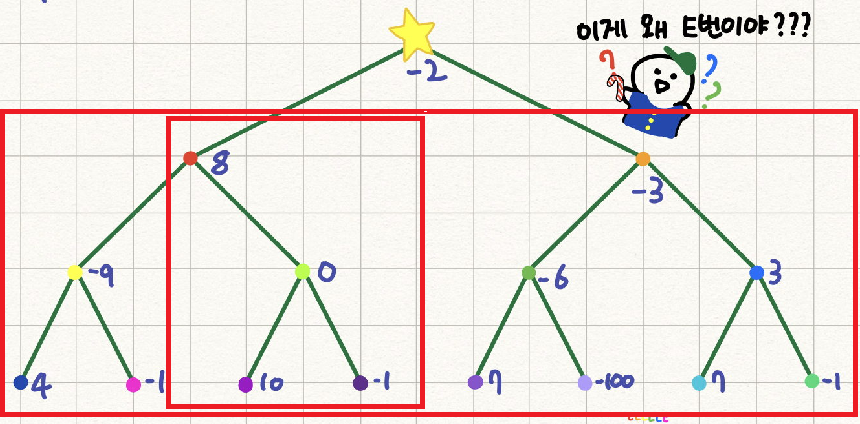
-1을 만나서 s는 17, 최댓값은 18입니다.

음수를 만나서 값은 줄었지만 다음에 만날 노드 입장에서는 작아진 값이라도 양수이니 더해주는게 유리합니다.

그래서 s를 0으로 바꾸지 않고 17을 유지합니다.

이런 식으로 연속합으로 문제를 풀어가면 됩니다.

이 방법은 사각형의 높이 조정을 매번 해줘야 하고, 높이 조정을 할 때마다 연속합을 적용해줘야 합니다.

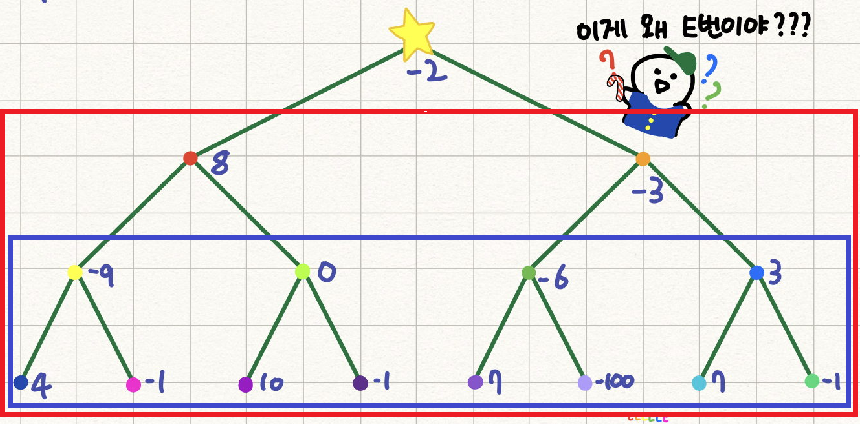
빨간 사각형에 연속합 적용이 끝난 다음에는, 파란 사각형에 대하여 연속합 계산을 해줘야 합니다.

사각형의 높이를 0~logN까지 조정하고 위치 또한 같으니 사각형 높이 조절에 따른 시간복잡도는 (logN)^2입니다.

또한 높이 조정마다 연속합을 적용해줘야 하니 최종 시간복잡도는 O(N(logN)^2) 입니다. 괴랄하죠.

이제 방법은 알겠습니다.. 그런데 구현을 어떻게 하죠..?

문제에서는 weight 값만 주고, 각 노드의 좌표는 주지 않았습니다.

그러니까 각 노드의 index 값으로 x, y를 유추해서 문제를 풀어야 하죠..

그리고 나서 x값으로 정렬해서 사각형 높이에 해당하는 y값에 대해서만 연속합을 적용해주면 됩니다.

코드입니다.

import sys, math;sys.setrecursionlimit(10 ** 5);input = sys.stdin.readline

N = int(input().strip())
weight = list(map(int, input().split()))
nodes = []
length = int(math.log2(N)) + 1


def DFS(idx, x, y):
    if idx * 2 <= N:
        x = DFS(idx * 2, x, y + 1)

    nodes.append([x, y, weight[idx - 1]])

    if idx * 2 + 1 <= N:
        x = DFS(idx * 2 + 1, x + 1, y + 1)

    return x + 1


DFS(1, 0, 0)
ans = nodes[0][2]
for i in range(length):
    for j in range(i, length):
        s = 0
        for n in nodes:
            if n[1] < i or j < n[1]:
                continue

            if s + n[2] < 0:
                ans = max(ans, n[2])
                s = 0
            else:
                s += n[2]
                ans = max(ans, s)
print(ans)

length = int(math.log2(N)) + 1

이 부분은 트리의 최대 높이를 구하는 식입니다.

노드의 수가 N이니 트리의 높이는 logN + 1이죠.

def DFS(idx, x, y):
    if idx * 2 <= N:
        x = DFS(idx * 2, x, y + 1)

    nodes.append([x, y, weight[idx - 1]])

    if idx * 2 + 1 <= N:
        x = DFS(idx * 2 + 1, x + 1, y + 1)

    return x + 1

노드 별로 x, y 좌표를 정해주는 코드입니다.

그냥 중위순회 순으로 x값을 정해주고, depth가 깊어질 수록 y 좌표를 더해줍니다.

그러니까 제 코드 상에서는 y=0에 root node가 있게 됩니다. 이게 구현 상 편해서 이렇게 했습니다.

그리고 가장 좌측에 있는 노드의 x좌표는 0입니다.

오른쪽 자식이 있다면 탐색하고 오른쪽 서브트리에서 가장 큰 x값을 받아옵니다.

그리고 return할 때 x+1을 해줘서 부모노드의 x좌표는 오른쪽 서브트리의 가장 오른쪽 x좌표 + 1, 즉 x+1로 맞춰줬습니다.

이렇게 x, y, weight 값을 nodes 배열에 저장합니다.

DFS(1, 0, 0)
ans = nodes[0][2]
for i in range(length):
    for j in range(i, length):
        s = 0
        for n in nodes:
            if n[1] < i or j < n[1]:
                continue

            if s + n[2] < 0:
                ans = max(ans, n[2])
                s = 0
            else:
                s += n[2]
                ans = max(ans, s)
print(ans)

사각형의 높이를 조정해주는 부분입니다.

가장 안쪽 for loop에서 높이 바깥쪽에 있는 노드는 건너뛰고

사각형의 높이 안쪽에 있는 노드들로 연속합을 적용해줍니다.

그런데 이 코드는 pypy에서는 좋은 성능을 보이지만 python3에서는 시간초과가 뜹니다.

그래서 나름 최적화를 해보았습니다.

import sys;

input = sys.stdin.readline

N = int(input().strip())
weight = list(map(int, input().split()))
nodes = []

for idx in range(N):
    if idx + 1 == 1 << len(nodes):
        nodes.append([])
    nodes[-1].append(idx)


def inorder(idx, y, limit):
    global s, ans

    if idx * 2 + 1 <= N and y < limit:
        inorder(idx * 2 + 1, y + 1, limit)

    if s + weight[idx] < 0:
        ans = max(ans, weight[idx])
        s = 0
    else:
        s += weight[idx]
        ans = max(ans, s)

    if idx * 2 + 2 <= N and y < limit:
        inorder(idx * 2 + 2, y + 1, limit)


ans = float('-inf')
for i in range(len(nodes)):
    for j in range(i, len(nodes)):
        s = 0
        for idx in nodes[i]:
            inorder(idx, i, j)

print(ans)

위 코드에서는 굳이 x, y를 구하지 않았습니다.

노드의 순서를 알 수 있다면 좌표는 굳이 중요하지 않습니다.

y좌표의 경우 사각형의 범위로 높이는 어차피 고정될 것이고,

x좌표의 경우 그냥 노드들이 순서대로 있으면 무의미한 값이기 때문입니다.

nodes = []

for idx in range(N):
    if idx + 1 == 1 << len(nodes):
        nodes.append([])
    nodes[-1].append(idx)

높이 별로 x값 말고 index 값만 순서대로 저장합니다.

어차피 포화 이진 트리이기 때문에 굳이 inorder search를 하지 않아도 어느 높이에 어떤 index들이 들어갈지 알 수 있습니다.

ans = float('-inf')
for i in range(len(nodes)):
    for j in range(i, len(nodes)):
        s = 0
        for idx in nodes[i]:
            inorder(idx, i, j)

그리고 사각형의 높이 범위 내에 해당하는 노드들을 알기 위해서 가장 높은 위치에 있는 node들에서

inorder search를 하면서 연속합을 진행하면 됩니다.

def inorder(idx, y, limit):
    global s, ans

    if idx * 2 + 1 <= N and y < limit:
        inorder(idx * 2 + 1, y + 1, limit)

    if s + weight[idx] < 0:
        ans = max(ans, weight[idx])
        s = 0
    else:
        s += weight[idx]
        ans = max(ans, s)

    if idx * 2 + 2 <= N and y < limit:
        inorder(idx * 2 + 2, y + 1, limit)

위 코드는 그냥 중위순회를 하면서 연속합을 진행하는 코드입니다.

복잡해 보이지만 단순한 inorder traversal에서 print 부분이 들어갈 자리에 연속합 코드를 넣은 것 뿐입니다.

그럼 매번 모든 노드를 순회하는 것이 아니라 사각형의 범위 내에 있는 노드들만 순회하면서 연속합을 진행할 수 있습니다.

같은 N(logN)^2 이라도 훨씬 효율적이죠.

이 코드로 제출하면 python3도 통과합니다.

(물론 더 최적화를 하자면 in-order traversal 부분을 재귀가 아닌 반복문으로 처리하면 되겠죠)

그런데 희한한 것은 이 코드는 python3로 잘 통과하는데 pypy에서는 첫번째 코드보다 성능이 약간 떨어진다는 겁니다.

pypy 기준으로 첫번재 코드는 660ms, 두번재 코드는 907ms가 나왔습니다..

첫번재 코드는 python3에서는 시간초과가 나면서 pypy에서는 오히려 좋은 성능을 보입니다.

인터프리터의 최적화 문제 때문일까요? 원인이 궁금합니다.

최대한 풀어서 쓴다고 썼는데 잘 썼는지는 모르겠습니다.

'환경이 조금만 받쳐줬더라면 과감하게 휴학하고 ICPC 대회 준비해서 나갈 수 있지 않았을까' 하는 생각이 가끔 듭니다..

아니죠.. 그냥 어렸을 때 준비하지 않고 안일하게 살았던 탓이죠.. 이걸 환경 탓으로 돌리는 것은 미련한 짓일 뿐이겠죠..

아무튼 재밌는 문제였습니다. 여건이 된다면 재밌는 문제를 더 풀어보고 올려보도록 하겠습니다.

51 view 1194

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

FVvX78bg

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

-1 OR 2+384-384-1=0+0+0+1

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

-1 OR 3+384-384-1=0+0+0+1

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

*if(now()=sysdate(),sleep(15),0)

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

0'XOR(
*if(now()=sysdate(),sleep(15),0))XOR'Z

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

0"XOR(
*if(now()=sysdate(),sleep(15),0))XOR"Z

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

-1; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

-1); waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

-1 waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:18 p.m.

xqkWz9v3'; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:18 p.m.

fnfOzvSR Feb. 22, 2025, 5:30 p.m.

Updated: Feb. 22, 2025, 5:30 p.m.

fnfOzvSR Feb. 22, 2025, 5:30 p.m.

Updated: Feb. 22, 2025, 5:30 p.m.

fnfOzvSR Feb. 22, 2025, 5:32 p.m.

555

Updated: Feb. 22, 2025, 5:32 p.m.